The Lebesgue-Cantor function

__________________________

Theorem

There exists a continuous monotone function

which is constant on every interval in

Proof:

Let be a decreasing sequence of closed sets used in the construction of the ternary Cantor set , so that

.

For , define

(the closure of the complement of ).

Note that

and so it consists of the closure of all intervals removed from [0,1] up to the -th step in the construction of the Cantor set.

It consists of disjoint intervals , ordered so that

.

Picture 1:

_______________

. ______ _______________ ______

. __ ______ __ _______________ __ ______ __ .

We define a sequence of monotone continuous functions as follows:

and

and

for

Picture 2:

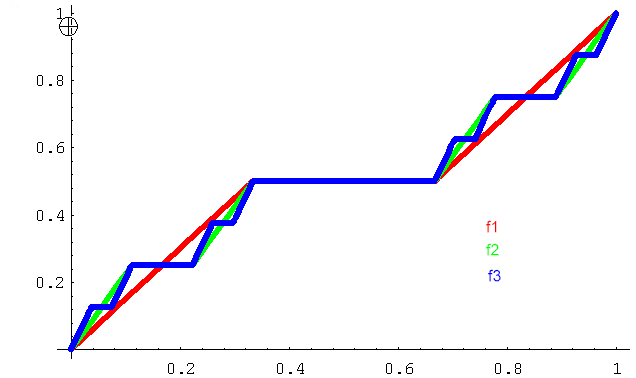
Note that if , then

.

Thus the sequence of monotone continuous functions , trivially converges on the set

and defines a continuous monotone function on this set. Since is dense in the function extends uniquely to the entire unit interval and has desired properties.