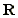 by
by
Nonmeasurable Sets
Theorem
There exist sets which are not Lebesgue
measurable.
Proof: (Vitali
1905)
Define an equivalence relation ~ on 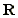 by
by
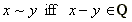 .
.
This relation divides  into
equivalence classes
into
equivalence classes 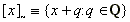 . Clearly each equivalence
class contains a point in the interval
. Clearly each equivalence
class contains a point in the interval 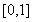 .
Let
.
Let 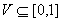 be a set which contains exactly one
point from each equivalence class. (By strong axiom of choice
be a set which contains exactly one
point from each equivalence class. (By strong axiom of choice
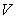 exist.)
exist.)
For all 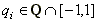 , define
, define
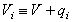 . (1)
. (1)
We observe that
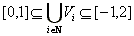 . (2)
. (2)
The second inclusion is clear. To see the first we
note that if 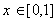 , then there must be a
, then there must be a 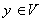 s.t.
s.t. 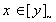 (because
(because 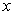 must belong some equivalence class and by our definition contains
one element from every equivalence class). Then
must belong some equivalence class and by our definition contains
one element from every equivalence class). Then 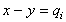 for some
for some 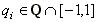 and thus we have
and thus we have
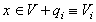 .
.
We note also that
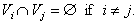 (3)
(3)
Otherwise for some 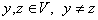 we would
have
we would
have  , which is impossible by our choice
of
, which is impossible by our choice
of 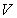 .
.
Now suppose 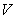 is measurable.
Then every
is measurable.
Then every 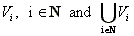 are.
are.
Using (2) and monotonicity property of the Lebesgue
measure 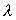 we would have
we would have
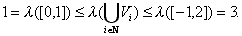 (4)
(4)
Also by translation invariance of the Lebesgue measure
we have
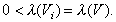 (5)
(5)
Therefore, using the fact that 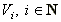 are pairwise disjoint and that the Lebesgue measure is
are pairwise disjoint and that the Lebesgue measure is 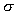 -additive,
we get that
-additive,
we get that
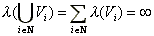 (6)
(6)
which contradicts (4).
Thus 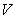 cannot
be measurable.
cannot
be measurable.