Dan Crisan
Professor of Mathematics
Imperial College London
Department of Mathematics
180 Queen's Gate
London SW7 2AZ, UK
d.crisan@imperial.ac.uk
0207 594 8489
Welcome to Dan Crisan's Homepage
I am currently a Professor of Mathematics in the Department of Mathematics at Imperial College London, where I also serve as Director of the EPSRC Centre for Doctoral Training in the Mathematics for our Future Climate: Theory, Data and Simulation (MFC CDT) (mfccdt.ac.uk).
The MFC CDT is a four-year, interdisciplinary PhD programme that harnesses mathematical theory, data, and simulation to address urgent challenges posed by climate change. It is jointly run by Imperial College London, the University of Reading, and the University of Southampton, working closely with partners across weather services, research institutions, business and industry, charities, and government. The programme offers fully funded PhD studentships. For more information about the MFC CDT, including the programme structure and how to apply, please visit mfccdt.ac.uk. In addition to my teaching and supervisory activities, I am one of the four Principal Investigators on the project Stochastic Transport in Upper Ocean Dynamics, a large-scale collaboration advancing our understanding of how randomness and turbulence shape the transport of heat, tracers, and pollutants in the oceans. This project has been awarded a prestigious six-year ERC Synergy Grant.
My long-term research interests lie broadly in Stochastic Analysis, a branch of mathematics concerned with understanding and modelling systems that evolve under the influence of randomness and uncertainty. Applications range from climate and geophysical fluid dynamics to finance and engineering.
To get an idea of my current research interests, here are some papers (for a complete list of publications please check my Google Scholar page) :
• Fluid Dynamics
- Theoretical and computational analysis of the thermal quasi-geostrophic model, D Crisan, DD Holm, E Luesink, PR Mensah, W Pan. Journal of nonlinear science 33 (5), 96. 2023. (journal link)
- An Implementation of Hasselmann’s Paradigm for Stochastic Climate Modelling, D. Crisan, D.D. Holm & P. Korn. 2023. (journal link)
- Variational principles for fluid dynamics on rough paths — D. Crisan, D.D. Holm, J.M. Leahy, T. Nilssen. Advances in Mathematics, 2022. (journal link)
- Semi-martingale driven variational principles — O.D. Street, D. Crisan. Proceedings of the Royal Society A, 2021. (journal link)
- Wave breaking for the Stochastic Camassa–Holm equation — D. Crisan, D.D. Holm. Physica D, 376:138–143, 2018. (journal link)
• Stochastic PDEs
- Global solutions for stochastically controlled fluid dynamics models, O Lang, D. Crisan, 2024, arXiv:2403.05923.
- Well-posedness properties for a stochastic rotating shallow water model — D. Crisan & O. Lang. *Journal of Dynamics and Differential Equations*, 2023. (doi link)
- Noise calibration for SPDEs: A case study for the rotating shallow water model D Crisan, O Lang, A Lobbe, PJ van Leeuwen, R Potthast Foundations of Data Science, 2023. (doi link)
- Analytical Properties for a Stochastic Rotating Shallow Water Model Under Location Uncertainty — O. Lang, D. Crisan & É. Mémin. 2023. (doi link)
- Solution properties of a 3D stochastic Euler fluid equation — D. Crisan, F. Flandoli, D.D. Holm. Journal of Nonlinear Science, 29(3):813–870, 2019. (doi link)
• Particle Representations / Approximations to (Stochastic) PDEs
- A Particle Filter for Stochastic Advection by Lie Transport (SALT): A case study for the damped and forced incompressible 2D Euler equation C Cotter, D Crisan, DD Holm, W Pan, I Shevchenko (doi link), 2020.
- D Crisan, J Miguez, Nested particle filters for online parameter estimation in discrete-time state-space Markov models doi link), 2018.
- D Paulin, A Jasra, D Crisan, A Beskos, Optimization Based Methods for Partially Observed Chaotic Systems, (doi link), 2019.
- Uniform in time estimates for the weak error of the Euler method for SDEs and a Pathwise Approach to Derivative Estimates for Diffusion Semigroups D Crisan, P Dobson, M Ottobre arXiv preprint arXiv:1905.03524
- D Crisan, C Janjigian, TG Kurtz, Particle representations for stochastic partial differential equations with boundary conditions, arXiv preprint arXiv:1607.08909
- Log-Normalization Constant Estimation Using the Ensemble Kalman–Bucy Filter with Application to High-Dimensional Models — D. Crisan, P. Del Moral, A. Jasra & H. Ruzayqat. 2022.
- Cubature on Wiener space for McKean–Vlasov SDEs with smooth scalar interaction — D. Crisan, E. McMurray. Annals of Applied Probability, 29(1):130–177, 2019.
- Two-dimensional pseudo-gravity model — J. Barré, D. Crisan, T. Goudon. Transactions of the AMS, 371(4):2923–2962, 2019.
- Numerical method for FBSDEs of McKean–Vlasov type — J.F. Chassagneux, D. Crisan, F. Delarue. Annals of Applied Probability, 29(3):1640–1684, 2018.
• Nonlinear Filtering
- Pathwise approximations for the solution of the non-linear filtering problem — D. Crisan, A. Lobbe, S. Ortiz-Latorre. In *Stochastic Analysis, Filtering and Stochastic Optimization* (commemorative volume to Mark H. A. Davis), 2022 https://arxiv.org/abs/2101.03957.
- A high-order time discretization of the solution of the non-linear filtering problem — D. Crisan, S. Ortiz-Latorre. Stochastics and PDEs: Analysis and Computation, 2019.
• Other (Preprints)
- Data assimilation for the stochastic Camassa–Holm equation using particle filtering: a numerical investigation — C.J. Cotter, D. Crisan & M.K. Singh. arXiv:2402.06927, 2024.
- Parallel sequential Monte Carlo for stochastic gradient-free nonconvex optimization — Ö.D. Akyildiz, D. Crisan, J. Míguez. Statistics and Computing, 30(6):1645–1663, 2020.
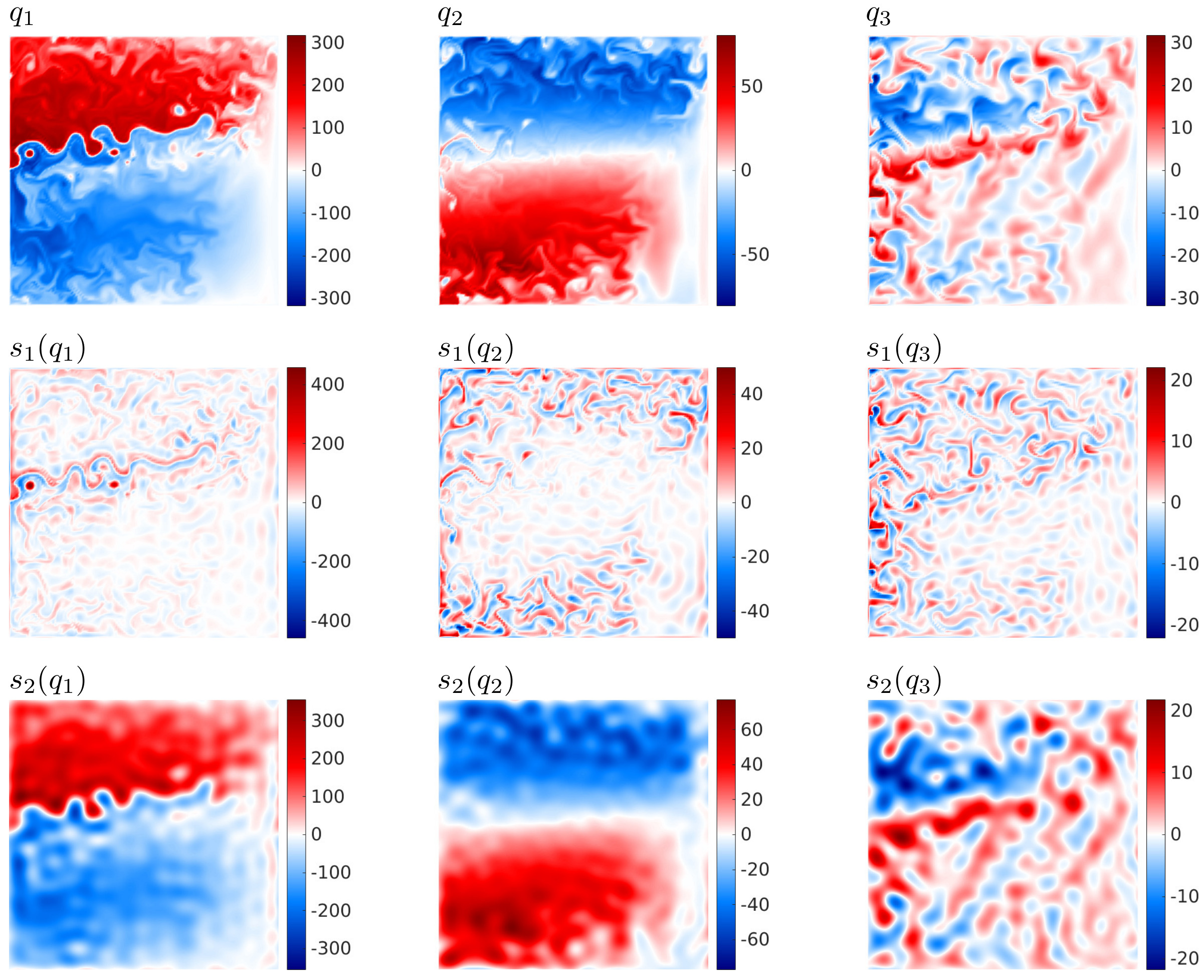
A representative snapshot of the potential vorticity, 𝐪, at different levels in the quasi-geostrophic three-layer model, along with its multiscale decomposition into scales s₁ ∈ [30, 300) km and s₂ ∈ [300, 3840] km. This is part of joint work with Igor Shevchenko (National Oceanographic Centre Southampton) The work was partially funded by the STUOD ERC Synergy project.
In addition, I completed a joint project with Colin Cotter and Darryl Holm, devoted to the development of rigorously validated Data Assimilation methodologies for high–dimensional systems. The project was funded by an EPSRC grant.