FTSE LACV at time 100

Let us plot the localized autocovariances in the style of a regular autocovariance plot with confidence intervals, to see whether the seemingly bigger values (at the right hand end) are significantly different from zero.

The left plot shows the localized autocovariance at time 100.

Well, the local autocovariance values are not exactly zero (and you'd expect that as they're random and computed from data). However, ALL the 95% confidence intervals completely cover the zero line. So, the conclusion is that NONE OF THEM are significantly different from zero.

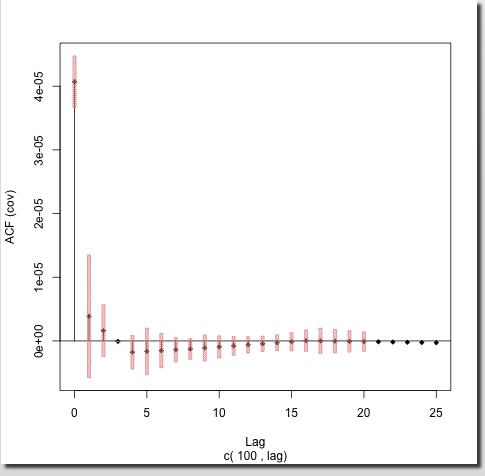
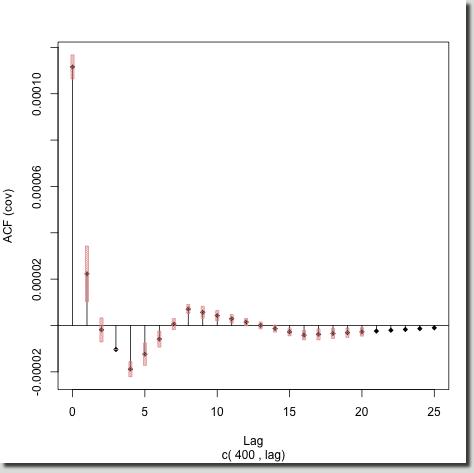
The right plot shows the local autocovariances for time 400.

Here, the lag one autocovariance's confidence interval does not overlap zero and hence we can conclude that the lag one autocovariance IS significantly different from zero, and actually the same is true for the lag four, five, six and some of the higher lags

Conclusion

Hopefully, this page and its examples will have convinced you of the usefulness of localized autocovariance and autocorrelation. If you have tested your time series for stationarity and it rejects stationarity then the localized tools above could be appropriate for, and give you insight into your data.

The localized autocovariances and their confidence intervals are produced using the Rvarlacv function in the locits package in R.